In programming, there are many ways to find an element in a given data structure, such as an array or list. However, as we shall see, not all of these are efficient. The easiest search algorithm is what we refer to as a sequential or linear search. As the name indicates, these algorithms check the elements sequentially, or one after another, in the order in which they appear in the list. The problem with this approach is efficiency. What if the element we are searching for is the last element in the list? In this case, we would have to search through all of the other elements before finally locating the element we are looking for. This may not be a problem if we are to search through 10 or 50 elements, but it is an entirely different story if the number is five million. To see examples of how to implement these algorithms, please read my article about sequential and linear search.

The binary search algorithm overcomes this limitation while remaining relatively low in complexity. To understand how the algorithm works, you can think of looking up a word in the dictionary; often you will open the dictionary at the middle and then, depending on the letter you find, determine whether you should look at the previous or next half. This simple process is repeated until you find the word you are looking for or determine that it is not there.

Performance

We will get back to the actual implementation, but first, let us consider what this means for us in terms of efficiency. While a linear or sequential search has a worst case scenario of N iterations (if the element we are searching for is the last one or not in the array at all), a binary search has a worst case of the logarithm of N. Therefore, we are facing a performance improvement from O(n) to O(log n) when looking at the Big O notation. If we have an array of 1024 elements, the maximum number of iterations (or method calls in the case of a recursive implementation) is log₂(1024) = 10 because 2¹⁰ = 1024.

This performance improvement is, in fact, crucial; the execution time of the search algorithm grows more and more slowly, whereas the linear search algorithm grows in a… linear fashion. This is shown in the figure below.

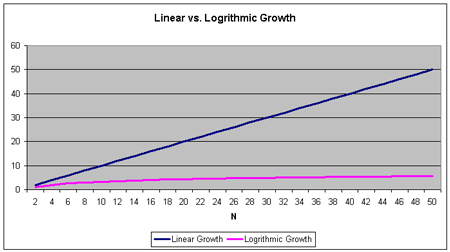
Source: MSDN

Therefore, the binary search algorithm is a very important concept in computer science and is used extensively in areas such as file systems and databases, which are usually implemented as tree data structures. These data structures rely on the concept of the binary search algorithm to ensure efficient operations. Unfortunately, this performance improvement does not come without a cost. Like with the dictionary example, this approach will only work if our data is sorted; if it is not, then there is no way to determine in which half of the data set the item we are looking for should be in. That is, we cannot disregard half of the remaining data set for each iteration. In most cases, however, the fact that the data set must be sorted is not a big issue; data is usually either stored sorted, or indexing schemes solve this issue. A database index, for example, ensures that a binary search can be used even when the physical data set is not sorted, thus ensuring O(log n) efficiency.

Implementations in PHP

There is more than one way to implement the binary search algorithm. It can be implemented either iteratively (by using a loop construct) or recursively. Below we will give examples on both of these implementations in PHP. As always, these algorithms can easily be rewritten to work in other programming languages.

Recursive Implementation

The first implementation that we will discuss is the recursive one. Discussing recursion is outside the scope of this article, but very simply put, then recursion is when a method invokes itself.

/**
 * Recursively searches for a value by using the binary search algorithm
 *
 * @var array $arr The array to search
 * @var mixed $value The value to search for
 * @var int $min The index to start the search at
 * @var int $max The index to stop the search at
 */
function binary_search_recursive(array $arr, $value, $min, $max) {
	// Base case: test if the range to search is empty
	if ($max < $min) {
		// The range to search is empty
		// That is, the value doesn't exist in the data set
		return false;
	}

	// Calculate the mid point of the set
	$middle = ceil((($min + $max) / 2));

	// Check if the value is potentially in the lower subset
	if ($arr[$middle] > $value) {
		// Search the lower subset for the key
		return binary_search_recursive($arr, $value, $min, ($middle - 1));
	}

	// Check if the value is potentially in the upper subset
	else if ($arr[$middle] < $value) {
		// Search the upper subset for the value
		return binary_search_recursive($arr, $value, ($middle + 1), $max);
	}

	// Otherwise, the value is on the index we are checking now
	else {
		// Value found. Return the value and end recursion
		return $arr[$middle];
	}
}

$arr = range(1, 1024); // Fill array with values from 1 to 1024
$result = binary_search_recursive($arr, 512, 0, (count($arr) - 1));

if ($result === false) {
	// Value not found; $result contains FALSE
} else {
	// Value found; it is contained in $result
}

To explain what happens in the above implementation, I will return to the dictionary example. Initially, all of the dictionary's words are candidates to be the one we are looking for, so just as we consider all indexes in the array above, we consider all of the words in the dictionary. First, we take a look in the middle of the book and check if the word we see is the one we are looking for. If not, then we check if the word we are looking for should exist earlier in the alphabet. We do this by comparing the current word with the word we are searching for. If this is case, then we can completely discard the last part of the book, because we have just established that the word must exist in the first half of the dictionary. Similarly, if the word cannot exist in the first half of the dictionary, we consider if it can exist in the last half. This can be done because the data set (the words in this case) are sorted alphabetically. If we were lucky enough to find the word we were looking for in the middle of the book, then there is nothing more to do. Otherwise we have to inspect the dictionary further by searching the appropriate half of it. This process continues until we either find the word or conclude that it does not exist in the dictionary. For every iteration that does not result in finding the word, we can classify half of the data set as being irrelevant in the search, which is what makes the algorithm logarithmic.

Now for the more technical explanation. The first thing we do in the algorithm is to check if the data set - or rather, range of indexes - to search is empty. If it is, then the value can obviously not exist. Remember that because the algorithm is recursive (that is, the method invokes itself), the size of this data set is reduced every time the method invokes itself. If this is not the case, then we calculate the middle of the data set. This is equivalent to looking up in the middle of a dictionary. In the code, we do integer comparisons, so we check if the value in the middle of the data set is greater than the value that we are looking for. If this is the case, then our value can only exist in the lower half of the data set. If not, we check if the value in the middle is less than our value. If that is the case, then our value can only exist in the upper half of the data set. If either of these two boolean expressions evaluate to true, then the appropriate subset of the data set is searched with the exact same logic (hence the recursion). Otherwise, the middle value must be the value we are looking for, and nothing more needs to be done.

Iterative Implementation

The same algorithm can also be implemented in an iterative fashion. That is, instead of having the method invoke itself, a loop is used.

/**
 * Iteratively searches for a value by using the binary search algorithm
 *
 * @var array $arr The array to search
 * @var mixed $value The value to search for
 * @var int $min The index to start the search at
 * @var int $max The index to stop the search at
 */
function binary_search_iterative(array $arr, $value, $min, $max) {
	$middle = 0;

	// Search until there are no more elements to check
	// The loop is terminated if the value is found
	while ($max >= $min) {
		// Calculate the mid point of the set
		$middle = ceil((($min + $max) / 2));

		// Check if the key is potentially in the lower subset
		if ($arr[$middle] > $value) {
			// Search the lower subset for the key
			$max = $middle - 1;
		}
		
		// Check if the key is potentially in the upper subset
		else if ($arr[$middle] < $value) {
			// Search the upper subset for the key
			$min = $middle + 1;
		}

		else {
			// Value found. Return it and terminate loop
			return $arr[$middle];
		}
	}
	
	return false; // Value not found
}

$arr = range(1, 1024); // Fill array with values from 1 to 1024
$result = binary_search_iterative($arr, 512, 0, (count($arr) - 1));

if ($result === false) {
	// Value not found; $result contains FALSE
} else {
	// Value found; it is contained in $result
}

The theory that supports this implementation is exactly the same; as such, the data set to search is cut in half for every iteration of the loop. The difference is simply that instead of invoking the method with different parameters, the parameters are simply changed for the next iteration of the loop. If the value can only be in the lower subset of the data set, then the maximum index is set to that of $middle - 1. This ensures that the next iteration only operates on the lower subset. Similarly, the minimum index is set to $middle + 1 if the value can only be in the upper subset. Narrowing the range of indexes thus ensures that the loop is one step closer to terminating, at which point the search is complete. If the value is found, it is returned, and the loop is thereby terminated.

Conclusion

As you have seen, then a simple algorithm can solve a fundamental problem in computer science and play a large role in all kinds of searches for data, be it in file systems, databases or anything else. The algorithm is very efficient - particularly when it operates on large data sets. In fact, it is best suited to be used on data sets that contain at least a few hundred items. The number of iterations or method invocations that are required to find a given item in a data set grows more slowly as the data set grows. This is because it is equivalent to the logarithm of N, where N is the total number of items in the data set. The maximum number of iterations or invocations would thus be 10 for a data set of 1024 items, for example, because the logarithm to the base of two of 1024 is 10. The worst case scenario for a linear search would be 1024 for the same data set. This efficiency particularly proves to be important when searching large data sets, which is often the case for databases, for instance. On very small data sets, a linear search may be slightly more efficient, but data sets often grow over time, so this advantage is hardly worth mentioning, and chances are that it will turn into a disadvantage over time.

This article discussed two different implementations of the algorithm; recursive and iterative, respectively. While the former may be slightly more complicated to implement for some people, it does also have a small disadvantage; it has a performance overhead due to the fact that it involves method invocations. This costs some additional resources because each invocation adds to the stack. However, since the number of invocations can ever be as high as the logarithm of the number of items in the data set, this is not a big concern. Most people do, however, consider the iterative approach to be easier to implement and understand, so the slight performance advantage is a bonus worth welcoming.